The Short Answer

A calculation method is analytical when results are computed using formulas derived from some kind of mathematical analysis. For example, if λ is the failure rate of a component, then the reliability of the component for mission time t is R(t) = exp{-λt}. The numerical result for R(t) can be obtained by computing exp{-λt} with the specified numerical values of λ and t. In general, analytical methods are quick and accurate. However, analytical methods are feasible only if there are no complex dependencies.

Simulation is when results are computed by mimicking the dynamic behavior of a system. In its broader sense, simulation is the process of observing the dynamic behavior of a system with varying sets of inputs. In reliability engineering, there is almost always randomness in the system behavior. Thus, to mimic this behavior, simulation requires random numbers as inputs. Simulation that involves random numbers is known as Monte Carlo simulation. Simulation is preferred if analytical methods are infeasible or so complex that results are prone to numerical round-off errors.

The Details

The formulas used in analytical methods to find numerical results are typically simple and convenient, making it possible to find exact results. If a system is complex, the resulting formulas may become complex, making the computational process lengthy and the results prone to round-off errors. In such circumstances, results may not be exact.

In general, computing results using explicit closed-form expressions is inefficient for complex systems because of long computation times and results that are prone to round-off errors. To improve the computations, researchers have proposed several algorithms to compute results more quickly and accurately. Windchill RBD uses such advanced algorithms whenever applicable. For example, Windchill RBD computes results using one such advanced algorithm named the Pivotal decomposition method whenever applicable.

It is difficult to find an exact analytical expression or algorithm for every scenario. It is particularly difficult when complex dependencies exist. Such dependencies may include warm standby components, shared repair resources, repair actions based on the state of the system, imperfect maintenance actions, priorities in selecting the paths in a network, and general failure/repair distributions.

To overcome the difficulties in analyzing systems with complex dependencies, a basic type of simulation known as crude Monte Carlo simulation can be used to compute results. To increase the efficiency, various improvements are proposed to the simulation process. They include variance reduction techniques, such as importance sampling, and special types of simulation methods for computing steady-state results. Relex RBD uses such types of advanced methods whenever applicable.

Simulation is based on the statistical concept that when the number of trials of an experiment approaches infinity, the average of the experiment 's outcome is equivalent to the expected value of the random variable under study. When availability is computed, the outcome is either system success or failure. The average of this outcome is the expected portion of success states, i.e., availability.

In reality, performing an infinite number of simulations is impossible. Therefore, an appropriate number of iterations must be specified. Determining the number of simulation iterations that will produce results conforming to the required accuracy within a reasonable computational time is important. This value varies, depending on several parameters.

Example

A simple example will be used to demonstrate how to evaluate the time-specific availability of the one component system in the RBD below.

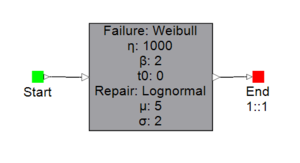
Distribution information for failure and repair times is provided in the above figure. The default value for the number of iterations is 1000, and the random number seed is 1. Using these values, the availability result is 0.731. Is this the true value for availability? To answer this question, use a seed of 2 to evaluate availability again. The availability result is 0.726, which is a difference of 0.005. The answer varies with the seed because the sequence of random numbers used in the simulation process is different. So, what is the true value of availability? As mentioned previously, simulation produces accurate results only when the number of iterations is large. When this is the case, the result does not depend on the seed because all possible sequences of random numbers produce the same availability value.

If the number of iterations is 10,000,000 rather than the default of 1000, the result for availability is 0.735914 with a random seed of 1. If we use a seed of 2 and compute availability again, the result is 0.736025. The difference in results is 0.000111, which is much less than 0.005. In general, the difference decreases as the number of iterations increases. (It should be noted that increasing the number of iterations increases the computational time.)

The effects of randomness on the results can be measured with the variance of the simulation output and the confidence intervals on the availability results. The confidence intervals are the range of availability values, bounded above and below, within which the true availability value is expected to fall with a certain percentage of confidence. The width of the confidence intervals is directly proportional to the standard deviation (square root of variance). The standard deviation is inversely proportional to the square root of the number of simulations. Therefore, increasing the number of simulation iterations by 4 times generally reduces the standard deviation to approximately 50%. Hence, the width of the confidence intervals is reduced to 50%. Reducing the standard deviation also decreases the width of the confidence intervals. Therefore, the number of iterations can be adjusted so that the confidence intervals are within the required accuracy.

How to Determine the Number of Simulations Needed

Assume that you want to find the availability of the single component system above within ±1% accuracy with a 95% confidence. First, compute the availability and 95% confidence intervals with 1000 iterations. The results are:

• Availability = 0.731
• Availability LCI = 0.70351
• Availability UCI = 0.75849

The width of the confidence interval for availability is UCI - LCI (0.05498). The width is 7.5% of the availability (0.731). If the true value falls somewhere within this interval, then the maximum possible error is ±3.75% of the availability.

The true value falls within these bounds with the 95 percent confidence. Therefore, the maximum possible error in the availability results is ±3.75% with 95% confidence. It is 3.75 times the required accuracy of ±1%. To reduce the width of the intervals 3.75 times, you must increase the number of simulations to (3.75)^2 or approximately 14 times. Thus, compute the results with 14,000 simulations. The results are:

• Availability = 0.7355
• Availability LCI = 0.728192
• Availability UCI = 0.742808

The width of the interval is 0.014616. It is 1.98% of the availability estimate. Therefore, the maximum possible error is ±0.99% with 95% confidence. This procedure provides a quick way to determine the number of simulation iterations.

Conclusion

Simulation can be used for analyzing any system. However, the accuracy of the results depends on the number of iterations and the complexity of the system. To achieve the desired level of accuracy, the number of simulations can be determined as indicated above. Analytical methods based on advanced algorithms are, in general, quicker and produce more accurate results than simulation. Therefore, whenever possible, it is better to use analytical methods. However, if analytical results are not possible or prone to round-off errors, then simulation should be used.

For additional information about Windchill RBD (formerly Relex RBD) and how it can be used to evaluate system reliablity and availability, please visit www.crimsonquality.com/rbd.